Hydraulic plants for controllable pitch propellers

Enrico Ravina

DITEN, Polytechnic School, Genoa University –

The article analyses the general problems connected with the proportioning and the dynamic modelling of hydraulic plants for the attitude control of blades in naval controllable -pitch propellers, referring in particular to the dynamic analysis of components that have non-conventional characteristics. Those circuits have peculiar hydraulic features that need specifically oriented analyses.

In controllable pitch propellers, it is provided a suitable mechanical transmission for modifying the trim angle of blades according to the dynamic characteristics required to the propeller itself.

The modification of the blade pitch is usually implemented by the motion of a hydraulic actuator, positioned inside the hub or in the propeller axis. If the piston is outside the hub, the connection between piston and blades occurs through a rod positioned inside the axis. In case of piston inside the hub, the pipes for the oil delivery and discharge are instead housed inside the axis.

The use of the transmission rod limits the maximum applicable load: as a matter of fact, in big-size plants, or anyway with longer axis, the actuator is positioned inside the hub.

In case of actuator inside the hub, two possible attitudes are proposed: the piston can be placed immediately aft of the blades (like, for instance, in the Wartsila E-HUB solution) or in correspondence of the same (like, for instance, in the Wartsila D-HUB solution). In the first case, it is possible a bigger actuation area than in the second case; the operation pressure is therefore minor, equal to forty bars maximum. In the second phase, we obtain instead a more compact and lighter plant requiring a minor number of mechanical elements, but the actuation pressure is about the triple.

A more compact plant allows also limiting the efficiency decrease determined by the bigger d_h diameter of the hub in controllable pitch propellers (CPP) in comparison with fixed pitch propellers (FPP). Indicating with d the propeller diameter, we can state that if in FPP we have d_h/d ≤ 0.2, CPP reach values of d_h /d ≤ 0.27÷0.4. The linear motion of the actuator is converted into rotary motion of the blade by a mechanism constituted by a cross-head connected with a crank pin at the base of each blade. The blades and their base rotate around their own axis (spindle axis), usually orthogonal to the propeller axis. The connection between pitch and linear displacement of the piston can be determined according to the type of blade motion mechanism. The piston stroke depends then on the size of the hub mechanism and on the maximum pitch to be performed; as a matter of fact, it must be bigger in ships with more propellers to permit the flag position.

The control circuit

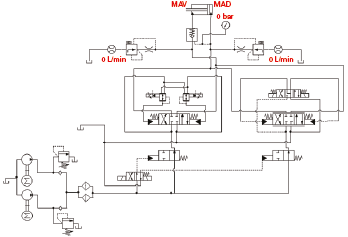
In this article we are considering a plant with actuator positioned in the hub; the operation principle of the hydraulic circuit is illustrated, in simplified form, in figure 1. The two chambers of the actuator are connected with the feeding and the discharge by two concentric pipes positioned inside the axis. A three-position distributor with four inlets, generally proportional, connects one or the other chamber to the feeding, depending on the pitch variation to be achieved. The propeller pitch is measured (feedback signal) and compared with the set pitch; the distributor spool is consequently moved upon control of a controller.

It is possible to find both open-centre and closed-centre solutions for the distributor. The closed-centre solutions allows discharging to the tank the flow rate processed by pumps where no flow is needed by the actuator. The oil transmission by the rotary part of the circuit to the fixed delivery and return pipes is implemented by a component called “Oil Distribution Box” (ODB), constituted by more rings communicating with the concentric pipes. The relative motion of the two parts of the ODB makes it difficult to realize efficient seals; this element is then subjected to notable flow rate losses.

The oil is transferred to the circuit by two positive-displacement pumps that suck oil from a tank.

Pumps are moved by electrical motors, generally asynchronous three-phase. In case of actuator inside the hub, this same circuit provides also for the lubrication of the hub mechanisms; to avoid the entry of water also in case of still pumps, the oil in the hub is always subjected to a static pressure, so that the tank is top-positioned on the floating line.

When the propeller has reached the desired pitch, it is possible to maintain its position if we prevent the actuator piston from discharging fluid into the tank, so that the action of the hydro-dynamic forces acting on the blade does not modify the pitch. This function is performed by the “counterbalance valve” (CBV), which prevents the oil from flowing out of the forward chamber if there is no feeding to the other chamber. This valve also allows maintaining the pitch in case of failure of the hydraulic plant. The CBV must be installed downstream the ODB to avoid that flow rate losses cause a motion of the actuator; in this way the system is only affected by the losses, very limited, inside the piston.

To make the operation of the circuit independent from the load, it is possible to install a load-sensing system, with the use of variable displacement pumps. Using instead a pressure balance before the distributor, we can keep the pressure difference constant at the two extremities of the same and make its operation more stable.

Due to the plant importance for the propulsion, the redundancy is applied by adopting two distributors. In this case, the emergency valve can be of “on/off” type; we prefer this solution for the minor cost and for the better reliability of on/off valves in comparison with proportional ones.

The position of the actuator piston, and consequently the reached pitch, is generally measured by a mechanical feedback. The system is constituted by a ring connected by an axis slot to the inner oil pipe. The ring position is detected by sensors outside the axis. In the case in which the ODB is positioned in correspondence of the reduction gear, or anyway at the axis extremity, the feedback can be induction type, with the advantage of operating without problems induced by friction phenomena.

The mechanical feedback is structurally simple but not very reliable because its position depends also on the pipe deformations caused by pressure and temperature variations. The problem can be limited by reducing, as far as possible, the pipe length.

A different solution uses a feedback by proximity sensors directly positioned in the hub. This system is more expensive also because it provides for some modifications to the inner hub design, but it is more reliable and precise. The propeller considered in this article is equipped with both mechanical and electrical feedbacks.

The valve control is performed by a controller, which compares the feedback signal with the chosen pitch; when the difference between the two exceeds the set accuracy, feeding is provided to the solenoid corresponding to the directional valve, in order to reduce the difference.

The dynamic model

The ODB has the function of transmitting the pressurized oil from the fixed pipes to the pipes that rotate with the propeller axis; it is constituted by rings that are filled by oil and are in communication with the axis interior. Owing to its function and the mechanical design difficulties, this element is typically affected by notable leakages. Leakages mainly depend on the fluid viscosity and then on the working temperature of the plant; besides, they are influenced by the axis rotation speed. To the ends of the simulation simplicity, we can consider that the axis rotates at constant speed: this is the case of operation at full capacity in presence of propulsion plant equipped with axis alternator, which generates electrical energy by exploiting the axis rotation. It is possible to model leakages like “spills” towards a tank, using valves for the flow rate control. In the valves usable as model, the flow rate Q is linked with the Δp pressure difference at the two extremities of the valve through the hydraulic coefficient.

In this case, a valve port is connected with the tank without further resistances and then the flow rate actually depends on the upstream pressure.

If true measurements of the ODB leakages are present, it is possible to impose a particular behaviour to the valve, that is to say to impose a flow rate-pressure curve. If only the data corresponding to an operation point are known, to deduce the flow rate-pressure curve we can impose that losses in correspondence of a foreseen operation pressure are equal to given ones and to draw an equivalent hydraulic coefficient. We can estimate the expected operation pressure, in first approximation as ratio between the force applied on the actuator and the area of the actuator itself. Afterwards, its value can be modified in the light of simulation results. Once deduced the hydraulic coefficient, we obtain a characteristic operation curve of the valve with a quadratic trend.

The actuator is a non-standard component, both by sizes and by structural shape; if positioned inside the hub, the geometry of the two chambers provides that the actuation areas are different. The sizes influence the hub diameter, which must be as small as possible not to worsen excessively the hydro-dynamic performances of the propeller.

The space that it is possible to take up with the actuator depends on its positioning, abaft or under the blades. Using modelling software supports that provide only for the presence of standard components, in first approximation it is possible to assimilate the real actuator with a standard actuator, imposing the equality of areas. The area of the backward chamber, which is the biggest of the two actuation areas, can be set equal to the major area of a standard cylinder and we draw the diameter from the equality. Setting the area of the forward chamber and the standard piston area equal, with piston diameter known, we can deduce an equivalent diameter for the rod. This model is usable for a first approximation sizing only; as a matter of fact, it is not possible to introduce other important parameters for the circuit operation, like for instance the chamber volume.

If the modelling software allows instead using, besides standard elements, base elements (area element, mass element, volume element etc.), we can implement models of not standardized actuators, able to approximate better the geometry of the real actuator.

The proportioning procedure is applied to a real case and validated by the use of two simulation codes: Automation Studio (developed by Famic Technologies, Canada) and Simulation X (developed by ITI GmbH, Dresden, Germany). The first is a code dedicated to the functional project and to the simulation of hydraulic and pneumatic circuits where the circuit of interest is created by standard components. The second, thanks to the use of standard elements included in the library, allows modelling with good accuracy not standardised components by shape and size.

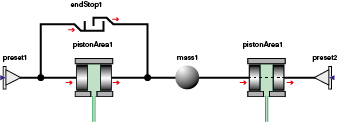
An example of not standardized component modelling

In Simulation X environment, the not standardized actuator, by shape and sizes, has been modelled with good accuracy. Referring to the figure 2, they have made use of elementary components like:

• “pistonArea”, which simulates the pressure acting on an area;
• “preset”, which puts a constraint to the motion;
• “mass”, which constitutes the mobile mass;
• “end stop”, which binds the relative motion between two components.

The “pistonArea” element is used to model the bind between a hydraulic pressure acting on an area and a mechanical force and to analyse then the resulting motion. It allows reproducing the balance of mechanical and hydraulic forces in linear actuators and for the modelling of spools or cartridges in valves where we want to study the behaviour in detail, if we cannot neglect the pressure forces acting on mobile parts.

Optionally, the element can also simulate the volume of contained fluid (variable according to the relative position of the two areas); in this case, we can set a “dead volume”, in order to make the model more complaint with the sizes of the real actuator.

Besides, we can consider the contact possibility between the two areas through the definition of a rigid or elastic “end stop” component. The geometrical parameters to be defined are the area and the initial relative position of the two areas. It is possible to calculate the area starting from the shape (circular or annular) or set in arbitrary way; with the latter option, it is possible to model a piston with not standard shape. The initial distance is assumed to be equal to half of the total stroke of the actuator, in order to set the “end stop” element more easily.

The volume calculation during the simulation is made according to the set area and the relative position of the two areas.

The results attainable from the simulation are:

• Pressure in the chamber
• Input flow rate
• volume
• relative position of the two areas
• speed difference
• force
• mechanical power

The “mass” element allows defining the mass of the mobile equipment, constituted by actuator piston, hub mechanism and concentric pipes. The mechanism housed in the hub has such a sizing as to bear the acting load and the actuation force; therefore, its weight is not negligible. Besides, also concentric pipes can have high lengths and then notable masses (sometimes up to 1000 kg), especially in case of twin-propeller ships or of ODB mounted in the reduction gear.

The “preset” element allows assigning a bind to a mechanical connection and then imposing a certain motion state to all the elements rigidly fixed on the mechanical junction considered. We can set fixed presets or with constant position, speed or acceleration. The motion of the elements mechanically connected with the preset exactly follows the set motion, irrespective of other forces eventually applied. In the actuator model, that element is used to block the position of the walls of the two chambers.

The “endStop” element is useful to impose a constraint to the relative motion of two mechanical components. It can be either elastic or rigid. If it is chosen rigid, the contact occurs like an ideal impact, with the momentum conservation. If we choose the elastic contact, the model includes a spring and a damper; nevertheless, in general, the parameters that allow characterizing them are of difficult determination. In the examined model, we preferred setting the operation as rigid. We can also take into account the friction present in the relative motion seats.

Results

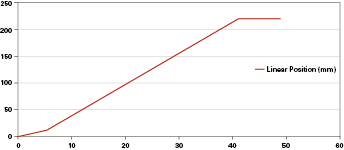
In figures 3 and 4, we report the linear displacement of the piston and the trend in time of the pressure in the backward chamber, deduced with the first of the two simulation codes.

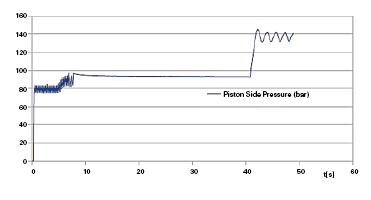
We can notice that in the instant in which the piston reaches the stroke end, if the pump remains in operation, the pressure increases up to making the maximum pressure valve intervene. This determines the pressure oscillations that we can notice in the final part of the simulation. In the initial portion, oscillations are due to the pressure transitory: since when the pump has been activated, the pressure gradually increases up to reaching such a value as to move the load; at this stage the piston moves causing a sudden pressure drop in the forward chamber; the pressure must grow again to move the load.

Another critical point concerns the opening or not of the CBV, which in the specific case opens the piloted one to allow the discharge from the backward chamber. The flow rate through the CBV is reported in figure 5.

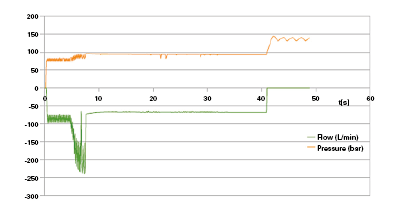
Besides, the piloting pressure is monitored by a pressure meter. It is also possible to control the flow rate through the pinch valve that models the ODB, to verify the adequacy of the model used.

Some conclusions

They have developed a model usable for the proportioning verification and for a preliminary dynamic analysis of circuits for the pitch control in controllable pitch propellers. The sizing procedure is verified, referring to a real case, by using “object oriented” codes, with modelling of not standardised components. The accuracy of the results is strongly influenced by the operating hypotheses assumed: in particular, the knowledge of the hydro-dynamic force distribution on the blade assumes relevance. This suggests a further development based on the interaction of simulation and fluid-dynamic codes.